11261. Cutting a stick

You need to cut a wooden stick into pieces. The most affordable company, The Analog Cutting Machinery, Inc. (ACM), charges money based on the length of the stick being cut. Their procedure requires making only one cut at a time.

It is easy to see that different choices of the cutting order lead to different costs. For example, consider a stick of length 10 meters that needs to be cut at 2, 4, and 7 meters from one end. Consider a few options:

· You could cut first at 2 meters, then at 4 meters, and finally at 7 meters. This would result in a cost of 10 + 8 + 6 = 24, because the first piece was 10 meters, the second 8 meters, and the third 6 meters.

· In another option, if you first cut at 4 meters, then at 2 meters, and finally at 7 meters, the cost would be 10 + 4 + 6 = 20, which is the better price.

Your boss trusts your computing skills to determine the minimal cost of cutting the given stick.

Input. Consist of several test cases. The first line of each test case contains the length of the stick l (l < 1000) that needs to be cut. The next line contains the number of cuts n (n < 50) to be made.

The following line contains n positive integers c_i (0 < c_i < l), representing the positions for the cuts, given in strictly increasing order. A line with l = 0 denotes the end of the input data.

Output. Print the minimal cost of cutting the stick in the format given in the example.

Sample input	Sample output
100 3 25 50 75 10 4 4 5 7 8 0	The minimum cutting is 200. The minimum cutting is 22.

SOLUTION

dynamic programming

Algorithm analysis

Let the array m contain the cutting points: m₁, …, m_n. Add the start and end points: m₀ = 0 and m_n+1 = l.

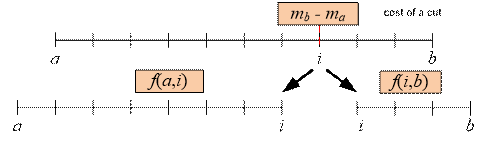
Let the function f(a, b) return the minimal cost of cutting a stick from m_a to m_b considering the necessary cutting points within the segment. There are no cutting points within the segment [m_a; m_{a + 1}], so f(a, a + 1) = 0. The solution to the problem will be the value of f(0, n + 1). Store the computed values of f(a, b) in the cells of the array dp[a][b].

Let the segment of the stick [m_a, m_b] be cut into several pieces. If the first cut is made at point m_i (a < i < b) , the cost of the cut itself will be m_b – m_a. Then, the remaining pieces need to be cut at the costs f(a, i) and f(i, b), respectively. Choose i to minimize the total cost:

f(a, b) = + m_b – m_a

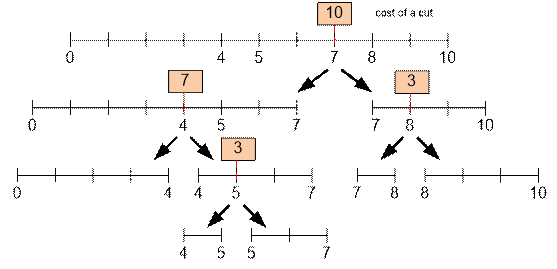
Example

Consider the second test case. Here is one possible way to cut a stick of length 10 with a cost of 10 + 7 + 3 + 3 = 23:

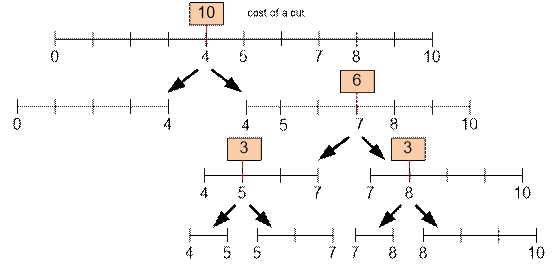
Now, consider the optimal way to cut the stick, which has a cost of 10 + 6 + 3 + 3 = 22:

Algorithm implementation

Declare constants and arrays.

#define MAX 55

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

int m[MAX];

The function f(a, b) returns the minimum cost of cutting a piece of stick on the segment [a; b] at the cutting points located inside the segment.

int f(int a, int b)

{

If a + 1 = b, then there are no cutting points within the segment [a; b]. Return 0.

if (b - a == 1) return 0;

If the value of f(a, b) is already computed, return it.

if (dp[a][b] != INF) return dp[a][b];

Make a cut at the point i (a < i < b). Compute the cost as follows:

f(a, b) = + m_b – m_a

for (int i = a + 1; i < b; i++)

dp[a][b] = min(dp[a][b], m[b] - m[a] + f(a, i) + f(i, b));

Return the result f(a, b) = dp[a][b].

return dp[a][b];

}

The main part of the program. Read the input data for each test case.

while (scanf("%d",&l),l)

{

scanf("%d",&n);

Add the start and end cutting points: m₀ = 0, m_n+1 = l.

m[0] = 0; m[n+1] = l;

for (i = 1; i <= n; i++)

scanf("%d",&m[i]);

Initialize the dp array.

memset(dp,0x3F,sizeof(dp));

Find and print the answer.

printf("The minimum cutting is %d.\n",f(0,n+1));

}